Интеграл — что это такое? Значение слова, определение, происхождение, перевод

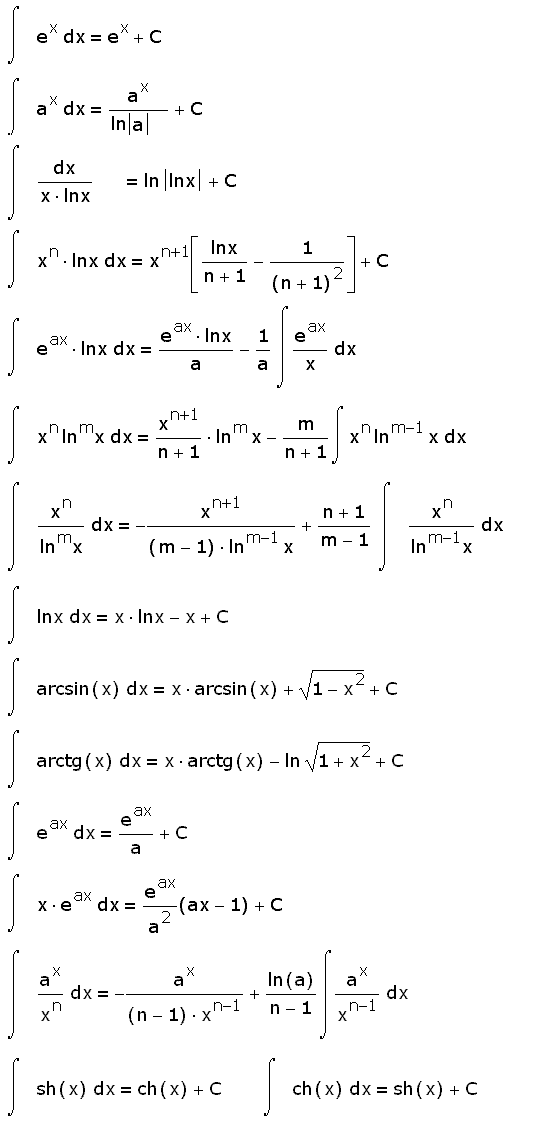
Интеграл это результат непрерывного суммирования бесконечно большого числа бесконечно малых слагаемых. При интегрировании функции берутся бесконечно малые приращения её аргументов и вычисляется бесконечая сумма приращений функции на этих участках. В геометрическом смысле удобно думать об интеграле двухмерной функции на определённом участке как о площади фигуры, замкнутой между графиком этой функции, осью X и перпендикулярными ей прямыми, соответствующими выбранному интервалу.

Пример: проинтегрируем функцию Y = X²
на интервале от X=2 до X=3.
Для этого нам нужно вычислить первообразную интегрируемой функции и взять разность её значений для концов интервала. Получаем:
X³/3 в точке X=3 принимает 9,
а в точке X=2 имеем 8/3.
Поэтому значение нашего интеграла: 9 - 8/3 = 19/3 ≈ 6.33.